GEMM based on the RISC-V Vector Extension (Part 1)

We will describe several times floating-point matrix multiplication kernels based on the RISC-V Vector Extension. In Part 1, we created double-, single- and half-precision floating-point matrix multiplication kernels for arbitrary matrix sizes and evaluated their performance using Ara’s RTL simulator.

Goal

The goal is to create floating-point matrix multiplication kernels based on the RISC-V Vector Extension and evaluate their performance using Ara’s RTL simulator.

Specifically, it targets GEMM (GEneral Matrix-to-matrix Multiply) compatible matrix multiplication kernels for BLAS (Basic Linear Algebra Subprograms). We also refer to the cblas_[d|s|h]gemm as a concrete API, where d, s and h represent double-, single- and half-precision floating-point respectively.

Below is the prototype declaration of cblas_dgemm in Netlib.

void cblas_dgemm(CBLAS_LAYOUT    layout,
                 CBLAS_TRANSPOSE TransA,
                 CBLAS_TRANSPOSE TransB,
                 const CBLAS_INT M,
                 const CBLAS_INT N,
                 const CBLAS_INT K,
                 const double    alpha,
                 const double*   A,
                 const CBLAS_INT lda,
                 const double*   B,
                 const CBLAS_INT ldb,
                 const double    beta,
                 double*         C,
                 const CBLAS_INT ldc);

The processing is as follows.

C = alpha * op(A) * op(B) + beta * C
with op(A) = [M x K], op(B) = [K x N], C = [M x N]

op(A) uses A as is when TransA is CblasNoTrans, and uses transposed A when TransA is CblasTrans. The same is true for op(B).

The simplified matrix product C = A * B corresponds to when both TransA and TransB are CblasNoTrans, alpha is 1.0 and beta is 0.0.

Ara

Ara is an implementation of the RISC-V Vector Extension (RVV) developed by the PULP (Parallel Ultra Low Power) project. Ara supports RVV v1.0.

Ara is characterized by its long VLEN (bit length of each vector register), and the default VLEN is 4096-bit even in a 256-bit configuration with four 64-bit Vector Units. Each vector register can handle 64 elements of double-precision floating-point, so if 32 vector registers are fully utilized, 2048 elements of double-precision floating-point can be handled.

Ara’s repository also has fmatmul, a double-precision floating-point matrix multiplication kernel. However, it is quite simplistic and has many issues for GEMM compatibility, such as not supporting arbitrary matrix sizes.

GEMM on Ara RTL Simulator

The prototype declaration of dgemm implemented in Part 1 is as follows. As of Part 1, transposition, alpha and beta are not supported.

void dgemm(const CBLAS_INT M,
           const CBLAS_INT N,
           const CBLAS_INT K,
           const double*   A,
           const CBLAS_INT lda,
           const double*   B,
           const CBLAS_INT ldb,
           double*         C,
           const CBLAS_INT ldc);

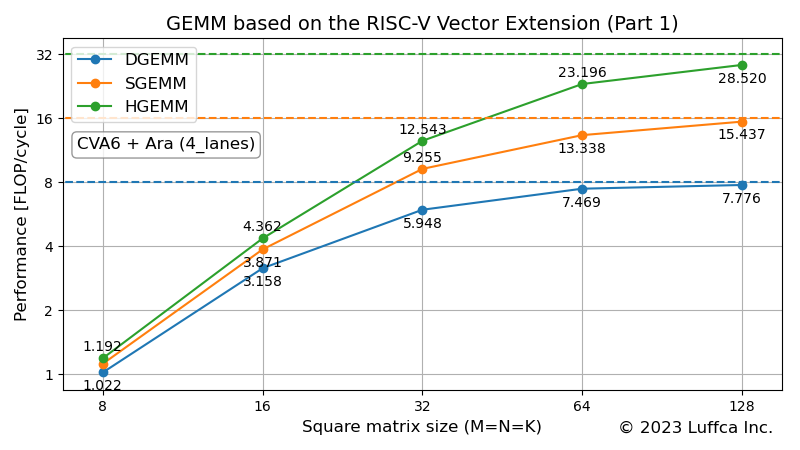
The featured image shows the performance of the double-, single- and half-precision floating-point matrix multiplication kernels in Ara’s 4_lanes (256-bit with four 64-bit Vector Units) configuration. DGEMM, SGEMM and HGEMM correspond to double-, single- and half-precision floating-point matrix multiplication kernels respectively.

The table below shows the performance and utilization of DGEMM, SGEMM and HGEMM when the size of the square matrix (M=N=K) is 128.

	Performance (FLOP/cycle)	Utilization (%)
DGEMM	7.776	97.2
SGEMM	15.437	96.5
HGEMM	28.520	89.1

The utilization of DGEMM and SGEMM exceeds 95%, and the utilization of HGEMM is about 90%, so we can see that it is very efficient. Ara’s Vector Unit is equipped with FMA (Fused Multiply-Add), so even with a configuration of four 64-bit Vector Units, eight double-precision floating-point operations are possible per cycle. Therefore, the utilization (%) of DGEMM is 7.776 / 8 * 100 = 97.2. Similarly, for single- and half-precision, 16 and 32 floating-point operations per cycle are possible.

However, by supporting arbitrary matrix sizes, issues with Ara became apparent. One of them is poor utilization when the size of the square matrix is odd. The case of SGEMM is remarkable, the utilization of matrix size 64 exceeds 80%, while the utilization of matrix size 65 drops to about 50%. If workarounds can be taken, it recovers to nearly 65% of utilization for matrix size 66, but it seems difficult to keep high utilization all the time.

Summary

We created double-, single- and half-precision floating-point matrix multiplication kernels based on the RISC-V Vector Extension and evaluated their performance using Ara’s RTL simulator.