2023-04-22 / 最終更新日時 : 2023-04-21 admin Simulator

GEMM based on the RISC-V Vector Extension (Part 3)

RISC-Vベクトル拡張に基づく浮動小数点行列積カーネルについて、数回に渡ってお伝えしていきます。Part 3では、転置行列、alpha及びbetaに対応したGEMMを完成させ、AraのRTLシミュレータを用いて性能を評価しました。

関連記事のPart 1では、任意の行列サイズに対応した倍精度、単精度及び半精度浮動小数点行列積カーネルの性能を評価しています。また、Part 2では、転置行列対応のためにベクトルロード/ストア性能を評価しています。

Goal

ここでは、Part 1で設定したゴールの要点を再確認します。

ゴールは、RISC-Vベクトル拡張に基づく浮動小数点行列積カーネルを作成し、AraのRTLシミュレータを用いて、その性能を評価することです。

具体的には、BLAS（Basic Linear Algebra Subprograms）のGEMM（GEneral Matrix-to-matrix Multiply）互換の浮動小数点行列積カーネルを目標としています。

処理としては、以下のようになります。

C = alpha * op(A) * op(B) + beta * C
with op(A) = [M x K], op(B) = [K x N], C = [M x N]

op(A)は、TransAがNのときはAをそのまま使用し、TransAがN以外のときは転置したAを使用します。op(B)も同様です。

Implementation of GEMM

ここでは、Part 3におけるGEMMの実装について見てゆきます。

Part 1において実装した単精度浮動小数点行列積カーネルSGEMMのプロトタイプ宣言は、以下のようになっていました。Part 1の時点では、転置行列、alpha及びbetaには対応していません。

// C = A * B
void sgemm(const CBLAS_INT M,
           const CBLAS_INT N,
           const CBLAS_INT K,
           const float*    A,
           const CBLAS_INT lda,
           const float*    B,
           const CBLAS_INT ldb,
           float*          C,
           const CBLAS_INT ldc);

Part 3において実装したSGEMMのプロトタイプ宣言は、以下のようになっています。転置行列、alpha及びbetaがサポートされており、ゴールに設定したGEMM互換であることが分かります。

// C = alpha * op(A) * op(B) + beta * C
void sgemm(CBLAS_TRANSPOSE TransA,
           CBLAS_TRANSPOSE TransB,
           const CBLAS_INT M,
           const CBLAS_INT N,
           const CBLAS_INT K,
           const float     alpha,
           const float*    A,
           const CBLAS_INT lda,
           const float*    B,
           const CBLAS_INT ldb,
           const float     beta,
           float*          C,
           const CBLAS_INT ldc);

実装したGEMMの処理の流れを擬似コードで表すと、以下のようになります。

// C = alpha * op(A) * op(B) + beta * C

// 1st block (C = beta * C)
if (beta != 1.0) {
  if (beta == 0.0) {
    C = 0.0
  } else {
    C = beta * C
  }
}

// 2nd block (AB = op(A) * op(B))
if (TransB != 'N') {
  // AB = A * Bt
  Bt = transpose(B)
  if (TransA != 'N') {
    AB = matmul_tn(A, Bt)
  } else {
    AB = matmul_nn(A, Bt)
  }
} else {
  // AB = A * B
  if (TransA != 'N') {
    AB = matmul_tn(A, B)
  } else {
    AB = matmul_nn(A, B)
  }
}

// 3rd block
C = alpha * AB + C

実装したGEMMの処理は、3つのブロックに分かれています。第1ブロックと第2ブロックは、それぞれC = beta * CとAB = op(A) * op(B)に関する処理を実行します。第3ブロックは、第1及び第2ブロックの結果とalphaを用いて、Cを算出します。

なお、第2ブロックでは、Part 2に記載したように、行列Bの転置が必要な場合、性能の低いストライドロード命令の使用回数を減らすため、予め転置行列B^T（疑似コードのBt）を作成しています。

GEMM on Ara RTL Simulator

ここでは、AraのRTLシミュレータを用いて、実装したGEMMの性能を見てゆきます。

はじめに、Part 3において実装したGEMMの浮動小数点演算（FLOP）数について検討します。今回実装したGEMMのFLOP数は、第1ブロックのbetaの値によって変化します。このため、第2ブロックと第3ブロックのFLOP数だけを対象とします。第2ブロックのA * BのFLOP数は、Part 1の実装と同じく2MNKです。第3ブロックのC = alpha * AB + CのFLOP数は、行列Cの要素数MN分の乗算と加算が行われるため2MNです。この結果、今回実装したGEMMのFLOP数は、少なくとも2MNK + 2MNとなります。Performanceは、このFLOP数を用いて計算します。

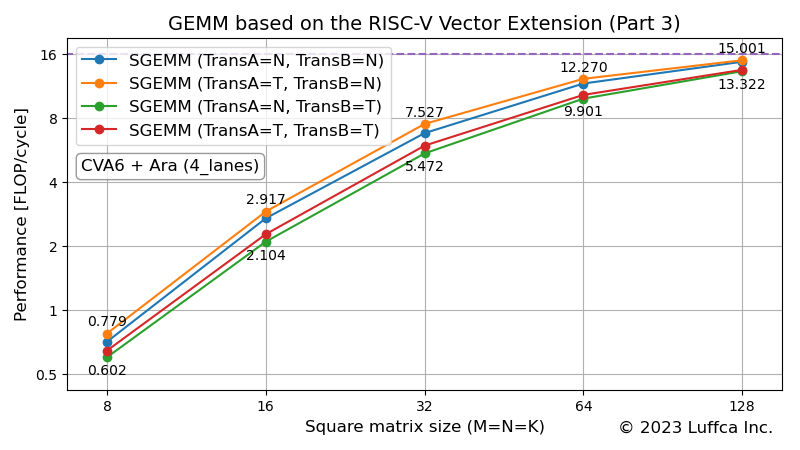
アイキャッチ画像は、Araの4_lanes（4つの64-bit Vector Unitを備えたベクトル演算幅256-bit）構成におけるSGEMMのPerformance（FLOP/cycle）を示しています。TransAとTransBの設定を表すNとTは、それぞれ転置無と転置有に対応しています。

また、アイキャッチ画像のPerformanceが16の破線は、ルーフラインを表しています。AraのVector Unitには、FMA（Fused Multiply-Add）が実装されているため、ベクトル演算幅256-bit構成でも、サイクル当たり16回の単精度浮動小数点演算が可能なことに対応しています。

以下の表は、正方行列（M=N=K）のサイズが128のときのSGEMMのPerformanceとUtilization（効率）を示しています。

	Performance (FLOP/cycle)	Utilization (%)
SGEMM (TransA=N, TransB=N)	14.756	92.2
SGEMM (TransA=T, TransB=N)	15.001	93.8
SGEMM (TransA=N, TransB=T)	13.322	83.3
SGEMM (TransA=T, TransB=T)	13.521	84.5

TransB=Nのグループの効率は92〜93%、TransB=Tのグループの効率は83〜84%であることが分かります。

なお、効率はPerformanceを理論性能で割った値です。ベクトル演算幅256-bit構成のAraでは、サイクル当たりの単精度浮動小数点演算の理論性能が16（FLOP/cycle）であることから、SGEMM（TransA=T, TransB=N）の効率（%）は、15.001 / 16 * 100 = 93.8となります。

Analysis of results

Support for transposed matrix

前述の表から、SGEMM（TransA=T, TransB=N）の効率が最も高く、SGEMM（TransA=N, TransB=T）の効率が最も低いことが分かります。ここでは、この結果を分析してゆきます。

表を詳細に見てゆくと、TransB=TのグループはTransB=Nのグループよりも効率が低くなっています。この原因は、Part 2に記載したように、行列Bの転置が必要な場合、性能の低いストライドアクセスの使用回数を減らすため、予め転置行列B^Tを作成する方法を選択したためです。正方行列サイズが128とき、転置行列B^Tの作成には、およそ30kサイクル必要なため、効率が約9%低下しています。

なお、正方行列サイズをnとすると、転置行列B^Tの作成に要するサイクル数がn²に比例するのに対し、行列積の演算量はn³に比例しています。このため、行列のサイズが大きくなるとTransB=Tのグループの効率は、TransB=Nのグループの効率に漸近してゆきます。

上記のTransB=Tのグループとは逆に、TransA=NのグループはTransA=Tのグループよりも僅かに（1.2〜1.5%）効率が低下しています。この原因も、行列Bと同様にストライドアクセスによるものです。但し、行列Aに対しては、TransA=Tのときに連続アクセス、TransA=Nのときにストライドアクセスが発生します。また、行列Aに対しては、最内ループにおいてロードされる要素数が少なく、Araのベクトルロード命令ではなく、プロセッサであるCVA6のロード命令によって要素がロードされています。

以上のことが、SGEMM（TransA=T, TransB=N）の効率が最も高く、SGEMM（TransA=N, TransB=T）の効率が最も低い原因です。なお、Part 1〜3におけるGEMMの実装は、列優先（row-major）の行列を前提としています。行優先（column-major）の行列の場合、今回の結果とは逆に、SGEMM（TransA=N, TransB=T）の効率が最も高く、SGEMM（TransA=T, TransB=N）の効率が最も低くなります。

Support for alpha and beta

ここでは、alphaとbetaのサポートの影響について見てゆきます。

alphaとbetaに対応していないPart 1のSGEMMでは、正方行列サイズが128ときの効率が96.5％でした。Part 3において実装したSGEMM（TransA=N, TransB=N）の効率は92.2％であり、効率が4.3%低下しています。

この原因としては、AraのAXIデータ幅がベクトル演算幅の半分に設定されていることが影響していると考えられます。

AXIデータ幅がベクトル演算幅の半分であっても、本実装の第2ブロックのAB = A * Bのように、ベクトル演算の要素数がロードする要素数の2倍以上であれば、メモリアクセスを隠蔽できます。

一方、第1ブロックのC = beta * Cや第3ブロックのC = alpha * AB + Cのように、ロード/ストアの要素数がベクトル演算の要素数の同等以上の場合、メモリアクセスに関わるロード/ストアのサイクル数がクリティカルパスとなって、効率が低下する結果となります。

まとめ

Luffcaでは、RISC-Vベクトル拡張に基づくGEMM互換の浮動小数点行列積カーネルを作成し、AraのRTLシミュレータを用いて性能を評価しました。

カテゴリー: Simulator

タグ: Benchmark RISC-V RISC-V Vector Verilator