GEMM based on the RISC-V Vector Extension (Part 1)
RISC-Vベクトル拡張に基づく浮動小数点行列積カーネルについて、数回に渡ってお伝えしていきます。Part 1では、任意の行列サイズに対応した倍精度、単精度及び半精度浮動小数点行列積カーネルを作成し、AraのRTLシミュレータを用いて性能を評価しました。
Goal
ゴールは、RISC-Vベクトル拡張に基づく浮動小数点行列積カーネルを作成し、AraのRTLシミュレータを用いて、その性能を評価することです。
具体的には、BLAS(Basic Linear Algebra Subprograms)のGEMM(GEneral Matrix-to-matrix Multiply)互換の浮動小数点行列積カーネルを目標としています。また、具体的なAPIとして、cblas_[d|s|h]gemmを参照しています。ここで、d、s及びhは、それぞれ倍精度、単精度及び半精度浮動小数点を表しています。
Netlibにおけるcblas_dgemmのプロトタイプ宣言は、以下のようになっています。
void cblas_dgemm(CBLAS_LAYOUT layout,
CBLAS_TRANSPOSE TransA,
CBLAS_TRANSPOSE TransB,
const CBLAS_INT M,
const CBLAS_INT N,
const CBLAS_INT K,
const double alpha,
const double* A,
const CBLAS_INT lda,
const double* B,
const CBLAS_INT ldb,
const double beta,
double* C,
const CBLAS_INT ldc);
処理としては、以下のようになります。
C = alpha * op(A) * op(B) + beta * C with op(A) = [M x K], op(B) = [K x N], C = [M x N]
op(A)は、TransAがCblasNoTransのときはAをそのまま使用し、TransAがCblasTransのときは転置したAを使用します。op(B)も同様です。
単純化された行列積C = A * Bは、TransAとTransBが共にCblasNoTrans、alphaが1.0、betaが0.0のときに対応します。
Ara
Araは、PULP(Parallel Ultra Low Power)プロジェクトで開発されているRISC-V Vector Extension(RVV)の実装です。Araは、RVV v1.0をサポートしています。
Araは、VLEN(各ベクトルレジスタのビット長)が長いことが特徴です。64-bit Vector Unitが4つの256-bitの構成でも、VLENのデフォルトは4096-bitです。各ベクトルレジスタで64要素の倍精度浮動小数点を処理できるので、32本のベクトルレジスタをフル活用できると、2048要素の倍精度浮動小数点を取り扱えることになります。
Araのリポジトリにも倍精度浮動小数点行列積カーネルのfmatmulがあります。但し、かなり単純化されていて、任意の行列サイズに対応していないなどGEMM互換に向けては多くの課題があります。
GEMM on Ara RTL Simulator
Part 1において実装したdgemmのプロトタイプ宣言は、以下のようになっています。Part 1の時点では、転置、alpha、betaには対応していません。
void dgemm(const CBLAS_INT M,
const CBLAS_INT N,
const CBLAS_INT K,
const double* A,
const CBLAS_INT lda,
const double* B,
const CBLAS_INT ldb,
double* C,
const CBLAS_INT ldc);
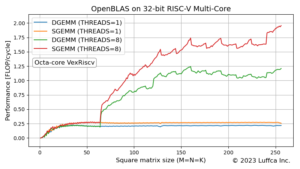
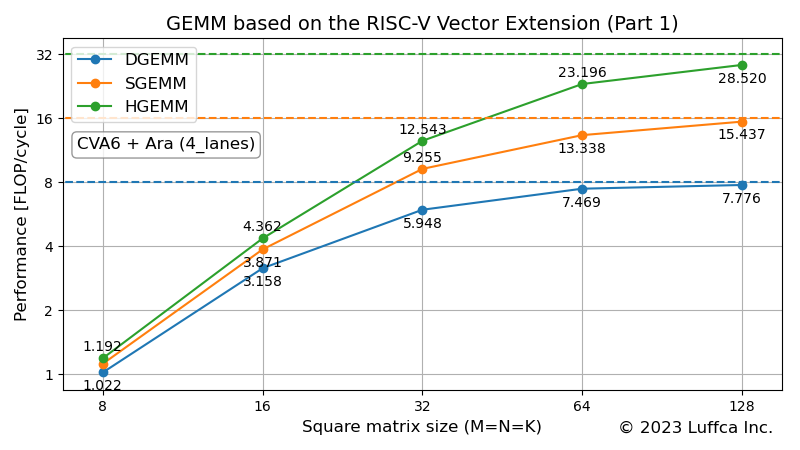
アイキャッチ画像は、Araの4_lanes(64-bit Vector Unitが4つの256-bit)構成における倍精度、単精度及び半精度浮動小数点行列積カーネルの性能を示しています。DGEMM、SGEMM及びHGEMMが、それぞれ倍精度、単精度及び半精度浮動小数点行列積カーネルに対応しています。
以下の表は、正方行列(M=N=K)のサイズが128のときのDGEMM、SGEMM及びHGEMMのPerformanceとUtilizationを示しています。
| Performance (FLOP/cycle) |
Utilization (%) |
|
|---|---|---|
| DGEMM | 7.776 | 97.2 |
| SGEMM | 15.437 | 96.5 |
| HGEMM | 28.520 | 89.1 |
DGEMMとSGEMMの効率は95%を超えており、HGEMMの効率はおよそ90%なので、非常に効率が良いことが分かります。なお、AraのVector Unitには、FMA(Fused Multiply-Add)が実装されているため、64-bit Vector Unitが4つの構成でも、サイクル当たり8回の倍精度浮動小数点演算が可能です。このため、DGEMMの効率(%)は、7.776 / 8 * 100 = 97.2となります。同様に、単精度と半精度の場合、サイクル当たり16回と32回の浮動小数点演算が可能です。
但し、任意の行列サイズに対応したことによって、Araの課題も見えてきました。その一つが、正方行列のサイズが奇数のときに、効率が低下することです。SGEMMの場合が顕著で、行列サイズ64の効率が80%を超えているのに対し、行列サイズ65の効率はおよそ50%にまで低下します。回避策を取れる場合、行列サイズ66の効率である65%近くまで回復しますが、常に高い効率をキープするのは難しいようです。
まとめ
Luffcaでは、RISC-Vベクトル拡張に基づく倍精度、単精度及び半精度浮動小数点行列積カーネルを作成し、AraのRTLシミュレータを用いて性能を評価しました。